• Maths 10th Class Coordinate Geometry

  Chapters

10th Class - Mathematics

  Share

10th Class - Mathematics
  • Text Book Solutions
  • Important Question
  • Question Papers / Notes Download

Solutions

NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry

NCERT Solutions Exercise 7.1 Class 10 Coordinate Geometry

Question 1.
Find the distance between the following pairs of points:
  • (i) (2, 3), (4, 1)
  • (ii) (-5, 7), (-1, 3)
  • (iii) (a, b), (-a, -b)
     

Solution:

Question 2.
Find the distance between the points (0, 0) and (36, 15).
 

Solution:
Let points be A (0, 0) and B (36, 15)
The distance between two points is

Question 3.
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
 

Solution:
Let points be A (1, 5), B (2, 3) and C (-2, -11)

AB + BC ≠ AC
Hence, the given points are not collinear.

Question 4.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
 

Solution:
Let points be A(5, -2), B (6, 4) and C (7, -2)

Here, AB = BC
ΔABC is an isosceles triangle.

Question 5.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in given figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.

Solution:
Points A (3, 4), B (6, 7), C (9, 4) and D (6, 1)

Here, AB = BC = CD = DA and AC = BD
ABCD is a square.
Hence, Champa is correct.

Question 6.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
  • (i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
  • (ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
  • (iii) (4, 5), (7, 6), (4, 3), (1, 2)
     

Solution:
(i) Let points be A (-1, -2), B (1, 0), C (-1, 2) and D (-3, 0)

Here, AC = BD, AB = BC = CD = AD
Hence, the quadrilateral ABCD is a square.
(ii) Let points be A (-3, 5), B (3, 1), C (0, 3) and D (-1, -4)

The given points do not form any quadrilateral.
(iii) Let points be A(4, 5), B (7, 6), C (4, 3) and D (1, 2)

Here, AB = CD, BC = AD
and AC ≠ BD
The quadrilateral ABCD is a parallelogram.

Question 7.
Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
 

Solution:
Let points be A (2, -5) and B (-2, 9)
Let P (x, 0) be the point on x-axis.
AP = BP

Question 8.
Find the values of y for which the distance between the points P (2, -3) and Q (10, y) is 10 units.
 

Solution:
Points P (2, -3), Q (10, y) and PQ = 10 units
The distance between two points is

Question 9.
If Q (0, 1) is equidistant from P (5, -3), and R (x, 6), find the values of x. Also find the distances QR and PR.
 

Solution:
Points are P (5, -3) and R (x, 6)
Point Q (0, 1) is equidistant from points P (5, -3) and R (x, 6).

Question 10.
Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4).
 

Solution:
Points A(3, 6) and B(-3, 4) are equidistant from point P(x, y)

NCERT Solutions Exercise 7.2 Class 10 Coordinate Geometry

Question 1.
Find the coordinates of the point which divides the join of (-1, 7) and (4, -3) in the ratio 2 : 3.
 

Solution:

Question 2.
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
 

Solution:

Question 3.
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in given
figure below. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5 th distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

Solution:
y-coordinate of green flag = 1/4 x 100 m = 25 m
Coordinates of green flag are P (2, 25)
y-coordinate of red flag = 1/5 x 100 = 20
Coordinates of red flag are Q (8, 20)
The distance between two points is

The blue flag is in the 5th line, at a distance of 22.5 m.

Question 4.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
 

Solution:
Let the required ratio be k : 1

Question 5.
Find the ratio in which line segment joining A (1, -5) and B (-4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.
 

Solution:

Question 6.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
 

Solution:

Question 7.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
 

Solution:

Question 8.
If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP = 3/7 AB and P lies on the line segment AB.
 
Solution:
Question 9.
Find the coordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts.
 

Solution:

Question 10.
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2, -1) taken in order.
[Hint: Area of a rhombus = 1/2 (product of its diagonals)]
 

Solution:

NCERT Solutions Exercise 7.3 Class 10 Coordinate Geometry

Question 1.
Find the area of the triangle whose vertices are:
  • (i) (2, 3), (-1, 0), (2, -4)
  • (ii) (-5, -1), (3, -5), (5, 2)
     

Solution:

Question 2.
In each of the following find the value of ‘k’ for which the points are collinear.
  • (i) (7, -2), (5, 1), (3, k)
  • (ii) (8, 1), (k, -4), (2, -5)
     

Solution:

Question 3.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
 

Solution:

Question 4.
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
 

Solution:

Question 5.
You have studied in Class IX, that a median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ABC whose vertices are A (4, -6), B (3, -2) and C (5, 2).
 
Solution:

NCERT Solutions Exercise 7.4 Class 10 Coordinate Geometry

Question 1.
Determine the ratio, in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).
 

Solution:
 

Question 2.
Find a relation between x and y, if the points (x, y), (1, 2) and (7, 0) are collinear.
 

Solution:

Question 3.
Find the centre of a circle passing through the points (6, -6), (3, -7) and (3, 3).
 

Solution:

Question 4.
The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.
 

Solution:

Question 5.
The class X students school in krishnagar have been alloted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m fron eaach other. There is trianguler grassy lawn in the plot as shoen in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.
 
  • (i) Taking A as origin, find the coordinates of the vertices of the triangle.
  • (ii) What will be the coordinates of the vertices of ?PQR, if C is the origin?

Also, calculate the areas of the triangles in these cases. What do you observe?

Solution

Question 6.
The vertices of a VABC are A(4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively. such that AD/AB=AE/AC=14. calculate the area of the ∆ADe and compare it with the area of ∆ABC.
 

Solution:

Question 7.
Let A(4, 2), B(6,5) and C(1, 4) be the vertices of ?ABC.
 
  • (i)The median from A meters BC at D. Find the coordinates ofthe point D.
  • (ii)Find the coordinates of the point P on AD, such that AP : PD = 2 : 1.
  • (iii)Find the coordinates of points Q and R on medians BE and CF respectively, such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
  • (iv)What do you observe?
  • [Note:The points which is common to all the three medians is called centroid and this point divides each median in the ratio 2 : 1]
  • (v)If A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC, find the coordinates of the centroid of the triangles.

Solution:

Question 8.
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1), P, Q, R and S are the mid-points of Ab, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
 

Solution:

Important Question

NCERT CBSE for Class 10 Maths Chapter 7 Coordinate Geometry Important Questions

Coordinate Geometry Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
Find the distance of the point (-3, 4) from the x-axis.
Year of Question:(2012OD)

Solution:
B(-3, 0), A (-3, 4)

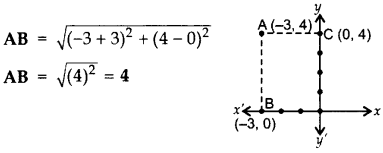
Question 2.
If the points A(x, 2), B(-3, 4) and C(7, -5) are collinear, then find the value of x.
Year of Question:(2014D)

Solution:
When the points are collinear,
x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2) = 0
x(-4 - (-5)) + (-3)(-5 - 2) + 7(2 - (-4)) = 0
x(1) + 21 + 42 = 0
x + 63 = 0 ∴ x = -63

Question 3.
For what value of k will k + 9, 2k - 1 and 2k + 7 are the consecutive terms of an A.P.?
Year of Question:(2016OD)

Solution:
As we know, a2 - a2 = a2 - a2
2k - 1 - (k + 9) = 2k + 7 - (2k - 1)
2k - 1 - k - 9 = 2k + 7 - 2k + 1
k - 10 = 8 ∴k = 8 + 10 = 18

Question 4.
In which quadrant the point P that divides the line segment joining the points A(2, -5) and B(5,2) in the ratio 2 : 3 lies?
Year of Question:(2011D)

Solution:

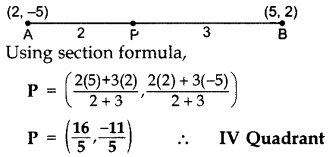
Question 5.
ABCD is a rectangle whose three vertices are B(4, 0), C(4, 3) and D(0, 3). Calculate the length of one of its diagonals.
Year of Question:(2014OD)

Solution:

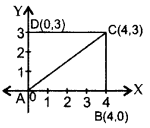
AB = 4 units BC = 3 units AC2 = AB2 + BC2 .[Pythagoras’theorem = (4)2 + (3)2 = 16 + 9 = 25 ∴ AC = 5 cm

Question 6.
In the figure, calculate the area of triagle ABC (in sq. units).
Year of Question:(2013D)

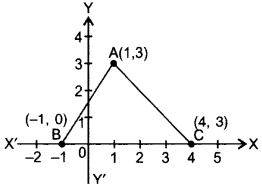
Solution:
Area of ∆ABC = 1/2 × base × corr, altitude
= 12 × 5 × 3 = 7.5 sq.units

Coordinate Geometry Class 10 Important Questions Short Answer-I (2 Marks)

Question 7.
Find a relation between x and y such that the point P(x, y) is equidistant from the points A (2, 5) and B (-3, 7).
Year of Question:(2011D)

Solution:
Let P (x, y) be equidistant from the points A (2, 5) and B (-3, 7).
∴ AP = BP .[Given
AP2 = BP2 .[Squaring both sides
(x - 2)2 + (y - 5)2 = (x + 3)2 + (y - 7)2
⇒ x2 - 4x + 4 + y2 - 10y + 25
⇒ x2 + 6x + 9 + y2 - 14y + 49
⇒ -4x - 10y - 6x + 14y = 9 +49 - 4 - 25
⇒ -10x + 4y = 29
∴ 10x + 29 = 4y is the required relation.

Question 8.
Find the relation between x and y if the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Year of Question:(2015OD)

Solution: When points are collinear,
∴ Area of ∆ABC = 0
= (x1 (y2 - y3) + x2(y3 - y1) + x3(y1 - y2)) = 0
= x (7 - 5) - 5 (5 - y) -4 (y - 7) = 0
= 2x - 25 + 5y - 4y + 28 = 0
∴2x + y + 3 = 0 is the required relation.

Question 9.
Find the ratio in which the point P(3/4,5/12) divides the line segment joining the points A(1/2,3/2) and B(2, -5).
Year of Question:(2015D)

Solution:

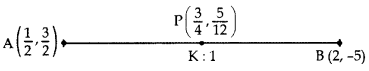
Let P divide AB in the ratio of K : 1.
Applying section formula,

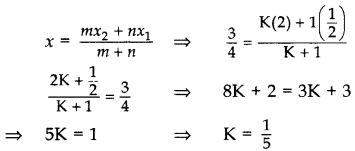
∴ Required ratio = 1 : 5

Question 10.
Find the ratio in which y-axis divides the line segment joining the points A(5, -6), and B(-1, -4). Also find the coordinates of the point of division.
Year of Question:(2016D)

Solution:

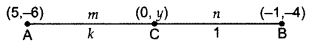
Let AC: CB = m : n = k : 1.

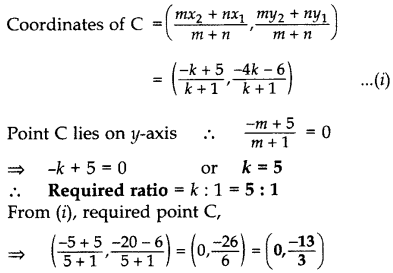
Question 11.
Let P and Q be the points of trisection of the line segment joining the points A (2, -2) and B (-7, 4) such that P is nearer to A. Find the coordinates of P and Question
Year of Question:(2016D)

Solution:

AP : PB = 1 : 2
Coordinates of P are:

Question 12.
Three vertices of a parallelogram taken in order are (-1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of fourth vertex.
Year of Question:(2011D)

Solution:
Let A(-1, 0), B(3, 1), C(2, 2) and D(x, y) be the vertices of a parallelogram ABCD taken in order. Since, the diagonals of a parallelogram bisect each other.
∴ Coordinates of the mid-point of AC = Coordinates of the mid-point of BD

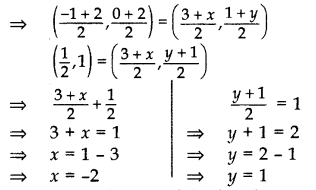
Hence, coordinates of the fourth vertex, D(-2, 1).

Question 13.
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, -5) is the mid point of PQ, then find the coordinates of P and Question
Year of Question:(2017OD)

Solution:

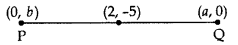
We know that at y-axis coordinates of points are (0, y) and at x-axis (x, 0).
Let P(0, b) and Q(a,0)
Mid point of PQ = (2, -5) .[Given

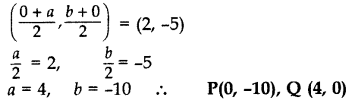
Question 14.
Determine the ratio in which the line 3x + y - 9 = 0 divides the segment joining the points (1, 3) and (2, 7).
Year of Question:(2011D)

Solution:
Suppose the line 3x + y - 9 = 0 divides the line segment joining A(1, 3) and B(2, 7) in the ratio k : 1 at point C.

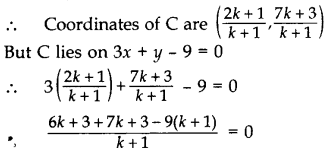
⇒ 6k + 3 + 7k + 3 - 9k - 9 = 0
⇒ 4k - 3 = 0
⇒ 4k = 3 ∴ k = 8
So, the required ratio is 3 : 4 internally.

Question 15.
If A(4, 3), B(-1, y) and C(3, 4) are the vertices of a right triangle ABC, right-angled at A, then find the value of y.
Year of Question:(2015OD)

Solution:
We have A(4, 3), B(-1, y) and C(3, 4). In right angled triangle ABC,
(BC)2 = (AB)2 + (AC).. [Pythagoras theorem
⇒ (-1 - 3)2 + (y - 4)2 = (4 + 1)2 + (3 - y)2 + (4 - 3)2 + (3 - 4)2 .(using distance formula
⇒ (-4)2 + (y2 - 8y + 16)
⇒ (5)2 + (9 - 6y + y2) + (1)2 + (-1)2
⇒ y2 - 8y + 32 = y2 - 6y + 36 = 0
⇒ -8y + 6y + 32 - 36
⇒ -2y - 4 = 0 ⇒ -2y = 4
∴ y = -2

Question 16.
If A(5, 2), B(2, -2) and C(-2, t) are the vertices of a right angled triangle with ∠B = 90°, then find the value of t.
Year of Question:(2015D)

Solution:

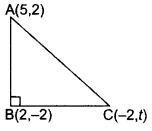
ABC is a right angled triangle,
∴AC2 = BC2 + AB2 .(i). (Pythagoras theorem
Using distance formula,
AB2 = (5 - 2)2 + (2 + 2)
= 25
BC2 = (2 + 2)2 + (t + 2)2
= 16 + (t + 2)2
AC2 = (5 + 2)2 + (2 - t)2
= 49 + (2 - t)2
Putting values of AB2, AC2 and BC2 in equation (i), we get
49 + (2 - t)2 = 16 + (t + 2)2+ 25
∴ 49 + (2 - t)2 = 41 + (t + 2)2
⇒ (t + 2)2 - (2 - t)2 = 8
⇒ (t2 + 4 + 4t - 4 - t2 + 4t) = 8
8t = 8 ⇒ t = 1

Question 17.
Find the area of the triangle whose vertices are (1, 2), (3, 7) and (5, 3).
Year of Question:(2011OD)

Solution:
Area of Triangle
= 1/2 [x1(y2 - y3) + x2(y3 - y1) + x3 (y1 - y2)]
= 1/2(1(7 - 3) + 3(3 - 2) + 5(2 - 7)]
= 1/2[4 + 3 + 5(-5)] = 18/2 = 9 sq. unit

Question 18.
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right triangle, right-angled at B. Find the value of p.
Year of Question:(2015OD)

Solution:
Similar to Question 16, Page 102.

Question 19.
Prove that the points (7, 10), (-2, 5) and (3, -4) are the vertices of an isosceles right triangle.
Year of Question:(2013D)

Solution:
Let A (7, 10), B(-2, 5), C(3, -4) be the vertices of a triangle.

. [By converse of Pythagoras theorem
∆ABC is an isosceles right angled triangle. .(ii) From (i) & (ii), Points A, B, C are the vertices of an isosceles right triangle.

Coordinate Geometry Class 10 Important Questions Short Answer-II (3 Marks)

Question 20.
Find that value(s) of x for which the distance between the points P(x, 4) and Q(9, 10) is 10 units.
Year of Question:(2011D)

Solution:
PQ = 10 .Given
PQ2 = 102 = 100 . [Squaring both sides
(9 - x)2 + (10 - 4)2 = 100.(using distance formula
(9 - x)2 + 36 = 100
(9 - x)2 = 100 - 36 = 64
(9 - x) = ± 8 .[Taking square-root on both sides
9 - x = 8 or 9 - x = -8
9 - 8 = x or 9+ 8 = x
x = 1 or x = 17

Question 21.
Find the value of y for which the distance between the points A (3,-1) and B (11, y) is 10 units.
Year of Question:(2011OD)

Solution:
AB = 10 units . [Given
AB2= 102 = 100 . [Squaring both sides
(11 - 3)2 + (y + 1)2 = 100
82 + (y + 1)2 = 100
(y + 1)2 = 100 - 64 = 36
y + 1 = ±6 . [Taking square-root on both sides
y = -1 ± 6 ∴ y = -7 or 5

Question 22.
The point A(3, y) is equidistant from the points P(6, 5) and Q(0, -3). Find the value of y.
Year of Question:(2011D)

Solution:
PA = QA .[Given
PA2 = QA2 . [Squaring both sides
(3 - 6)2 + (y - 5)2 = (3 - 0)2 + (y + 3)2
9 + (y - 5)2 = 9 + (y + 3)2
(y - 5)2 = (y + 3)2
y - 5 = ±(y + 3) . [Taking sq. root of both sides
y - 5 = y + 3 y - 5 = -y - 3
0 = 8 . which is not possible ∴ y = 1

Question 23.
If a point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), then find the value of p.
Year of Question:(2012D)

Solution:
Similar to Question 24, Page 103.

Question 24.
Find the value of k, if the point P(2, 4) is equidistant from the points A(5, k) and B(k, 7).
Year of Question:(2012OD)

Solution:
Let P(2, 4), A(5, k) and B(k, 7).

PA = PB .[Given
PA2 = PB2 . [Squaring both sides
(5 - 2)2+ (k - 4)2 = (k - 2)2 + (7 - 4)2
9 + (k - 4)2 - (k - 2)2 = 9
(k - 4 + k - 2) (k - 4 - k + 2) = 0
(2k - 6)(-2) = 0
2k - 6 = 0
2k = 6 ∴ k = 6/2 = 3

Question 25.
If the point P(k - 1, 2) is equidistant from the points A(3, k) and B(k, 5), find the values of k.
Year of Question:(2014OD)

Solution:
PA = PB .Given
PA2 = PB2 . [Squaring both sides
⇒ (k - 1 - 3)2 + (2 - k)2 = (k - 1 - k)2 + (2 - 5)2
⇒ (k - 4)2 + (2 - k)2 = (-1)2 + (-3)2
k2 - 8k + 16 + 4 + k2 - 4k = 1 + 9
2k2 - 12k + 20 - 10 = 0
2k2 - 12k + 10 = 0
⇒ k2 - 6k + 5 = 0 .[Dividing by
⇒ k2 - 5k - k + 5 = 0
⇒ k(k - 5) - 1(k - 5) = 0
⇒ (k - 5) (k - 1) = 0
⇒ k - 5 = 0 or k - 1 = 0
∴ k = 5 or k = 1

Question 26.
Find a point P on the y-axis which is equidistant from the points A(4, 8) and B(-6, 6). Also find the distance AP.
Year of Question:(2014OD)

Solution:

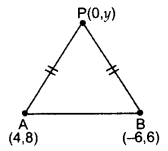
Let P(0, y) be any point on y-axis.
PA = PB . [Given
PA2 = PB2 . [Squaring both sides
⇒ (4 - 0)2 + (8 - y)2 = (-6 - 0)2 + (6 - y)2
16 + 64 - 16y + y2 = 36 + 36 + y2 - 12y
80 - 72 = -12y + 16y
8 = 4y ⇒ y = 2
∴Point P (0, 2).
Now, AP =√(4-0)2+(8-2)2
∴ Distance, AP = √16+36=√52

Question 27.
If the point P(x, y) is equidistant from the points A(a + b, b - a) and B(a - b, a + b), prove that bx = ay.
Year of Question:(2016OD)
Solution:
PA = PB . [Given
PA2= PB2 . [Squaring both sides
⇒ [(a + b) - x]2 + [(b a) - y)2 = [(a - b) - x]2 + [(a + b) - y]2
⇒ (a + b)2 + x2 - 2(a + b)x + (b - a)2 + y2 - 2(b - a)y = (a - b)2 + x2 - 2(a - b)x + (a + b)2 + y2 - 2(a + b)y .[∵ (a - b) 2= (b - a)2
⇒ -2(a + b)x + 2(a - b)x = -2(a + b)y + 2(b - a)y
⇒ 2x(-a - b + a - b) = 2y(-a - b + b - a)
⇒ -2bx = - 2ay
⇒ bx = ay (Hence proved)

Question 28.
If the point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), find p. Also find the length of AB.
Year of Question:(2014D)

Solution:
AB = AC . [Given
∴ AB2 = AC2.[Squaring both sides
⇒ (3 - 0)2 + (p - 2)2= (p - 0)2 + (5 - 2)2
⇒ 9+ (p - 2)2 = p2 + 9
⇒ p2 - 4p + 4 - p2 = 0
⇒ -4p + 4 = 0
⇒ -4p = -4 ⇒ p = 1

Question 29.
If the point P(2, 2) is equidistant from the points A(-2, k) and B(-2k, -3), find k. Also find the length of AP.
Year of Question:(2014D)
Solution:
PA = PB . [Given
PA2 = PB2 . [Squaring both sides
⇒ (2 + 2)2 + (2 - k)2 = (2 + 2k)2 + (2 + 3)2
16 + 4 + k2 - 4k = 4 + 4k2 + 8k + 25
4k2 + 8k + 25 - k2 + 4k - 16 = 0
3k2 + 12k + 9 = 0
⇒ k2 + 4k + 3 = 0 .[Dividing by 3
k2 + 3k + k + 3 = 0
k(k + 3) + 10k + 3) = 0
(k + 1) (k + 3) = 0
k + 1 = 0 ork + 3 = 0
i k = -1 or k = -3
AP = √(2+2)2+(2-k)2
When k = -1
AP =√16+(2+1)2=√16+9= 5 units
When k = -3
AP = √16+(2+3)2=√16+25 units

Question 30.
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right angled isosceles triangle.
Year of Question:(2016OD)

Solution:
Similar to Question 19, Page 102.

Question 31.
Prove that the points A(0, -1), B(-2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD.
Year of Question:(2013D)

Solution:

Opposite sides BC = AD = 4√5
Diag. AC = BD = 10
∴ABCD is a rectangle.
. [∵ Opp. sides are equal & diagonals are also equal

Question 32.
Show that the points (-2, 3), (8, 3) and (6, 7) are the vertices of a right triangle.
Year of Question:(2013D)

Solution:
Let A (-2, 3), B(8,3), C(6, 7).
(AB)2 = (8 + 2)2 + (3 - 3)2 = 102 + 02 = 100
(BC)2 = (6 - 8)2 + (7 - 3)2 = (-2)2 + 42 = 20
(AC)2 = (6 + 2)2 + (7 - 3)2 = 82 + 42 = 80
Now, (BC)2 + (AC)2= 20 + 80 = 100 = (AB)2
.[By converse of Pythagoras’ theorem
Therefore, Points A, B, C are the vertices of a right triangle.

Question 33.
Prove that the points A(2, 3), B(-2, 2), C(-1, -2) and D(3, -1) are the vertices of a square ABCD.
Year of Question:(2013OD)

Solution:
Given: A(2, 3), B(-2, 2), C(-1, -2), D(3, -1)

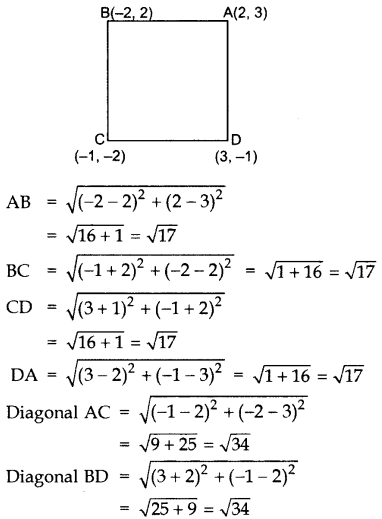
AB = BC = CD = DA .[All four sides are equal
AC = BD .[Also diagonals are equal
∴ ABCD is a Square.

Question 34.
Prove that the points A(2, -1), B(3, 4), C(-2, 3) and D(-3, -2) are the vertices of a rhombus ABCD. Is ABCD a square?
Year of Question:(2013OD)

Solution:

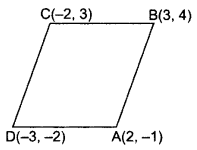
Given: A(2, -1), B(3, 4), C(-2,3), D(-3, -2)

Question 35.
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) & D(2,6), are equal and bisect each other.
Year of Question:(2014OD)

Solution:

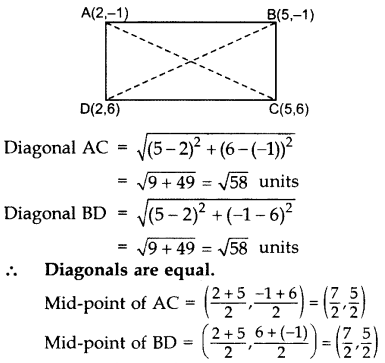
∴ Diagonals also bisect each other.
Question 36.
Find that value of k for which point (0, 2), is equidistant from two points (3, k) and (k, 5).
Year of Question: (2013OD)

Solution:
Similar to Question 29, Page 104.

Question 37.
If the points A(-2, 1), B(a, b) and C(4, -1) are collinear and a - b = 1, find the values of a and
Year of Question: (2014D)

Solution:
Since A(-2, 1), B(a, b) and C(4, -1) are collinear.
∴x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2) = 0
⇒ -2[b - (-1)] + a(-1 - 1) + 4(1 - b) = 0
⇒ -2b - 2 - 2a + 4 - 4b = 0
⇒ -2a - 6b = -2
⇒ a + 3b = 1 . [Dividing by (-2)
⇒ a = 1 - 3
We have, a - b = 1 .[Given
(1 - 3b) - b = 1 .[From (i)
1 - 3b - b = 1
-4b = 1 - 1 = 0 - b = 0/-4 = 0
From (i), a = 1 - 3(0) = 1 - 0 = 1
∴ a = 1, b = 0

Question 38.
If the points A(-1, -4), B(b, c) and C(5, -1) are collinear and 2b + c = 4, find the values of b and c.
Year of Question: (2014D)

Solution:
A(-1, -4), B(b, c), C(5, -1) are collinear.
∴x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2) = 0
⇒ -1(c + 1) + b(-1 + 4) + 5(-4 - c) = 0
⇒ -c - 1 - b + 4b - 20 - 5c = 0
⇒ 3b - 6c = 21
⇒ - b - 2c = 7 .[Dividing by 3
⇒ b = 7 + 2c
We have, 2b + c = 4 . [Given
2(7 + 2c) + c = 4 . [From (i)
⇒ 14 + 4c + c = 4
⇒ 5c = 4 - 14 = -10 ⇒ c = -2
⇒ b = 7 + 2(-2) = 3 . [From (i)
∴ b = 3, c = -2

Question 39.
Find the area of the triangle ABC with A(1, 4) and mid-points of sides through A being (2, -1) and (0, -1).
Year of Question: (2015D)

Solution:

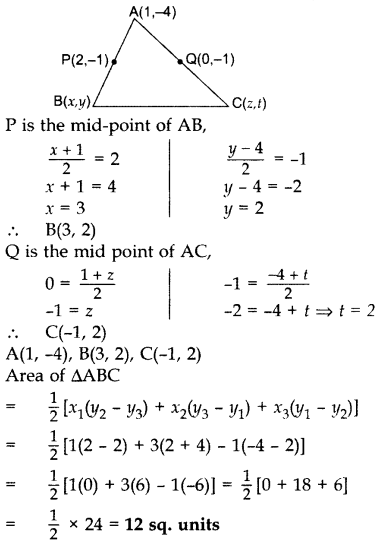
Question 40.
Find the area of the triangle PQR with Q(3, 2) and the mid-points of the sides through Q being (2, -1) and (1, 2).
Year of Question: (2015D)

Solution:
Let P(x, y), R(z, t).

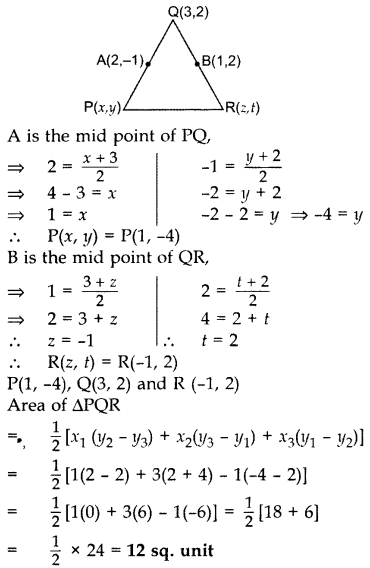
Question 41.
Find the ratio in which the y-axis divides the line segment joining the points (-4, -6) and (10, 12). Also find the coordinates of the point of division.
Year of Question: (2013D)

Solution:

Question 42.
Find the ratio in which point P(-1, y) lying on the line segment joining points A(-3, 10) and B(6, -8) divides it. Also find the value of y.
Year of Question: (2013D)

Solution:

Question 43.
In what ratio does the point (14.4) divide the line segment joining the points P(2, -2) and Q(3, 7)? Also find the value of y.
Year of Question: (2017OD)

Solution:

Question 44.
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) such that AP = AB.
Year of Question: (2015OD)

Solution:

Question 45.
Points A(-1, y) and B(5, 7) lie on a circle with centre 0(2, -3y). Find the values of y. Hence find the radius of the circle.
Year of Question: (2014D)

Solution:
Join OA and OB. .[radii of a circle
∴ OA = OB OA2 = OB2 .[Squaring both sides
⇒ (2 + 1)2 + (-3y - y)2 = (5 - 2)2 + (7 + 3y)2
⇒ 9+ (-4y)2 = 9 + (7 + 3y)2
⇒ 16y2 = 49 + 42y + 9y2
⇒ 16y2 - 9y2 - 42y - 49 = 0
⇒ 7y2 - 42y - 49 = 0
⇒ y2 - 6y - 7 = 0 .[Dividing both sides by 7
⇒ y2 - 7y + y - 7 = 0
⇒ y(y - 7) + 1(y - 7) = 0
⇒ (y - 7) (y + 1) = 0
y - 7 = 0 or y + 1 = 0
y = 7 or y = -1
(i) Taking y = 7

Question 46.
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a + b = 1, find the values of a and b.
Year of Question: (2014D)

Solution:
Similar to Question 37, Page 105.

Question 47.
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3,-2). If the third vertex is (7/2,y), find the value of y.
Year of Question: (2017D)

Solution:
Given: Area of ∆ = 5 sq. units
Vertices: (2, 1), (3, -2) and (7/2,y)
Area of ∆

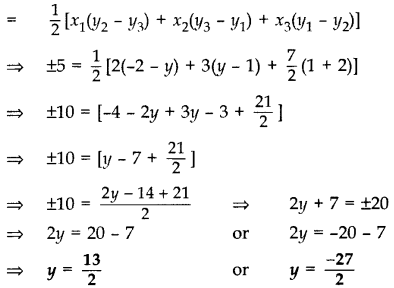
Question 48.
Find the ratio in which the line segment joining the points A(3, -3) and B(-2, 7) is divided by x-axis. Also find the coordinates of the point of division.
Year of Question: (2014OD)

Solution:
Similar to Question 41, Page 106.

Question 49.
In the Figure, ABC is a triangle coordinates of whose vertex A are (0, -1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the midpoint of BC, find the areas of ∆ABC and ∆DEF.
Year of Question: (2016D)

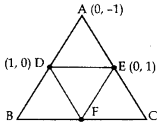
Solution:
Let B (p, q), C (r, s)
and F(x, y)
Mid-point of AB = Coordinates of D

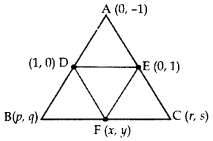
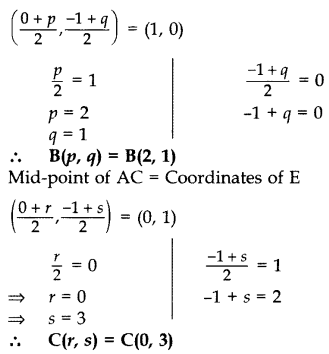
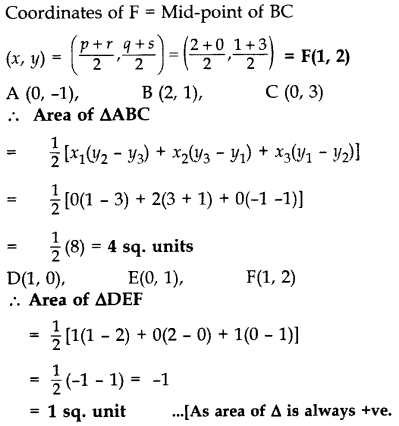
Coordinate Geometry Class 10 Important Questions Long Answer (4 Marks)

Question 50.
If the points A(x, y), B(3, 6) and C(-3, 4) are collinear, show that x - 3y + 15 = 0.
Year of Question: (2012OD)

Solution:
Pts. A(x, y), B(3, 6), C(-3, 4) are collinear.
∴ Area of ∆ = 0
As area of ∆
= 1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
∴Area of ∆ABC
= x(6 - 4) + 3(4 - y) + (-3) (y - 6) = 0
= 2x + 12 - 3y - 3y + 18 = 0
= 2x - 6y + 30 = 0
∴x - 3y + 15 = 0 . [Dividing both sides by 2

Question 51.
Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k - 1, 5k) are collinear.
Year of Question: (2015OD)

Solution:
A (k + 1, 2k), B(3k, 2k + 3) and C(5k - 1, 5k).
When points are collinear, area of ∆ is 0.
∴ Area of triangle = 0
⇒ [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
⇒ [(k + 1) (2k + 3 - 5k) + 3k (5k - 2k) + (5k - 1) (2k - 2k - 3)] = 0
⇒ [(k + 1) (3 - 3k) + 3k(3k) + (5k - 1)(-3)] = 0
⇒ [3k - 3k2 + 3 - 3k + 9k2 - 15k + 3) = 0
⇒ 6k2 - 15k + 6 = 0
⇒ 2k2 - 5k + 2 = 0
⇒ 2k2 - 4k - 1k + 2 = 0
⇒ 2k(k - 2) - 1(k - 2) = 0
⇒ (k - 2)(2k - 1) = 0
⇒ k - 2 = 0 or 2k - 1 = 0
⇒ k = 2 or k = 1/2
We get, k = 2, 1/2

Question 52.
If two vertices of an equilateral triangle are (3, 0) and (6, 0), find the third vertex.
Year of Question: (2011D)

Solution:
Let A (3,0), B (6, 0), C (x, y).
∴ ∆ABC is an equilateral
∴ AB = BC = AC
AB2 = BC2 = AC2 .[Squaring throughout
(6 - 3)2 + (0 - 0)2 = (x - 6)2 + (1 - 0)2 = (x - 3)2 + (y - 0)2
9 = x2 - 12x + 36 + y2 = x2 - 6x + 9 + y2

Question 53.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
Year of Question: (2011D)

Solution:

Question 54.
If the vertices of a triangle are (1, -3), (4, p) and (-9, 7) and its area is 15 sq. units, find the value(s) of p.
Year of Question: (2012D)

Solution:
Area of ∆ = 15 sq. units
12 [1(p - 7) + 4(7 + 3)) + (-9)(-3 - p)] = ±15
p - 7 + 40 + 27 + 9p = ±30
10p + 60 = ± 30
10p = -60 ± 30
p = -60±30/10
∴ Taking +ve sign, p = -60+30/10=-30/10 = -3
Taking -ve sign, p = -60-30/10=-90/10 = -9

Question 55.
For the triangle ABC formed by the points A(4, -6), B(3,-2) and C(5, 2), verify that median divides the triangle into two triangles of equal area.
Year of Question: (2013OD)
Solution:
Let A(4, -6), B(3, -2) and C(5, 2) be the vertices of ∆ABC.
Since AD is the median
∴ D is the mid-point of BC.
⇒ D(3+5/2,-2+2/2) ⇒ D(4,0)
Area of ∆ABD
= 1/2 [4(-2 - 0) + 3(0 + 6) + 4(-6 + 2)]
= 1/2 [-8 + 18 - 16) = 1/2 [-6] = -3
But area of A cannot be negative.
∴ ar(∆ABD) = 3 sq.units .(i)
Area of ∆ADC
= 1/2 [4(0 - 2) + 4(2 + 6) + 5(-6 - 0)]
= 1/2(-8 + 32 - 30] = 1/2 [-6] = -3
But area of ∆ cannot be negative.
∴ ar(∆ADC) = 3 sq.units
From (i) and (ii),
∴ Median AD of AABC divides it into two ∆s of equal area.

Question 56.
If A(4, 2), B(7,6) and C(1, 4) are the vertices of a AABC and AD is its median, prove that the median AD divides AABC into two triangles of equal areas.
Year of Question: (2014OD)

Solution:

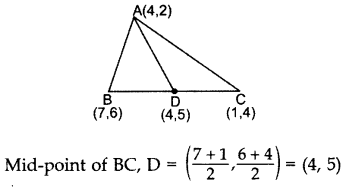
Area of ∆ABD
= 1/2 (x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
= 1/2[4(6 - 5) + 7(5 - 2) + 4(2 - 6))
= 1/2(4 + 21 - 16) = 9/2 sq.units .(i)
Area of ∆ADC
= 1/2 [4(5 - 4) + 4(4 - 2) + 162 - 5)]
= 1/2(4 + 8 - 3) = 92sq.units
From (i) and (ii),
Area of ∆ABD = Area of ∆ADC
∴ Median AD divides ∆ABC into two triangles of equal area.

Question 57.
Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units.
Year of Question: (2015OD)

Solution:
Let A(k + 1, 1), B(4, -3) and C(7, -k).
We have, Area of ∆ABC = 6 . [Given
6 = 1/2 [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
6 = 1/2[(k + 1)(-3 + k) + 4(-k - 1) + 7(1 + 3)]
12 = (-3k + k2 - 3 + k - 4k - 4 + 28]
12 = [k2 - 6k + 21]
⇒ k2 - 6k + 21 - 12 = 0
⇒ k2 - 6k + 9 = 0
⇒ k2 - 3k - 3k + 9 = 0
⇒ k(k - 3) - 3(k - 3) = 0 =
⇒ (k - 3) (k - 3) = 0
⇒ k - 3 = 0 or k - 3 = 0
⇒ k = 3 or k = 3
Solving to get k = 3.

Question 58.
Prove that the area of a triangle with vertices (t, t - 2), (t + 2, t + 2) and (t + 3, t) is independent of t.
Year of Question: (2016D)

Solution:
Let A(t, t - 2), B(t + 2, + + 2), C(t + 3, t).
Area of ∆ABC
= 1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
= 1/2 [t(t + 2 - t) + (t + 2)(t - (t - 2)) +(t + 3)((t - 2) - (t + 2))]
= 1/2 [t(2) + (t + 2)(2) + (t + 3)(-4)]
= 1/2 (2+ + 2+ + 4 - 46 - 12] = 12 [-8] = -4
Area of ∆ is always positive.
∴ Area of ∆ = 4 sq. units, which is independent of t.

Question 59.
If the centroid of ∆ABC, in which A(a, b), B(b, c), C(c, a) is at the origin, then calculate the value of (a3 + b3 + c).
Year of Question: (2012OD)

Solution:

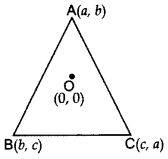
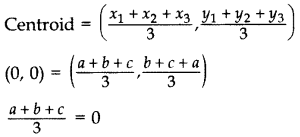
a + b + c = 0
If a + b + c = 0
then, as we know
a3 + b3 + c3 - 3abc = (a + b + c)(a2 + b2 + c2 - ab - bc - ac) ∴ a3 + b3 + c3 - 3abc = 0 . [Since a + b + c = 0
∴a3 + b3 + c3 = 3abc .(Hence proved)

Question 60.
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 or x + y = -9.
Year of Question: (2013D)

Solution:
Let A(x, y), B(1, 2), C(2, 1).
Area of ∆ABC = 6 sq. units .[Given
As 1/2 [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)] = 6
∴ x(2 - 1) + 1(1 - y) + 2(y - 2) = ±12
x + 1 - y + 2y - 4 = ±12
Taking +ve sign
x + y = 12 + 4 - 1
∴ x + y = 15
Taking -ve sign
x + y = -12 + 4 - 1
∴ x + y = -9

Question 61.
In the given figure, the vertices of ∆ABC are A(4, 6), B(1, 5) and C(7, 2). A line segment DE is drawn to intersect the sides AB and AC at D and E respectively such that AD/AB=AE/AC=1/3. Calculate the area of ∆ADE and compare it with area of ∆ABC.
Year of Question: (2016OD)

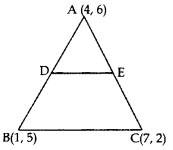
Solution:
AD : AB = 1 : 3; AE : AC = 1 : 3
∴ AD : DB = 1 : 2; AE : EC = 1 : 2

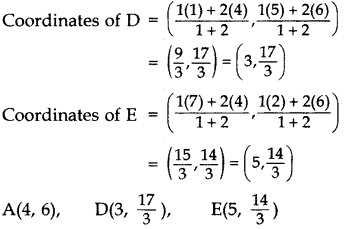
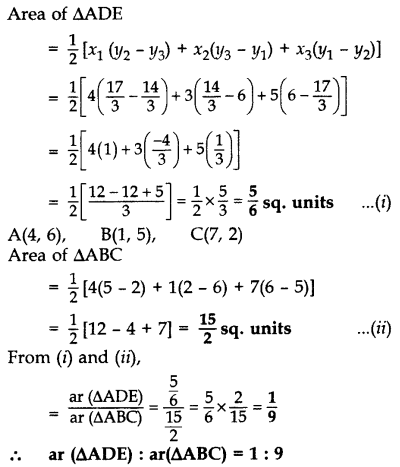
Question 62.
Point P(x, 4) lies on the line segment joining the points A(-5, 8) and B(4, -10). Find the ratio in which point P divides the line segment AB. Also find the value of x.
Year of Question: (2011OD)

Solution:

Question 63.
A point P divides the line segment joining the points A(3, -5) and B(-4, 8) such that AP/PB=K/1. If P lies on the line x + y = 0, then find the value of K.
Year of Question: (2012D)

Solution:

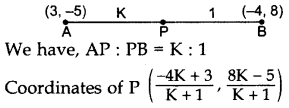
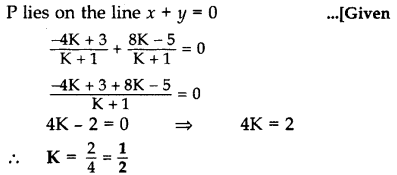
Question 64.
Find the ratio in which the point P(x, 2) divides the line segment joining the points A(12, 5) and B(4, -3). Also, find the value of x.
Year of Question: (2014D)

Solution:

Question 65.
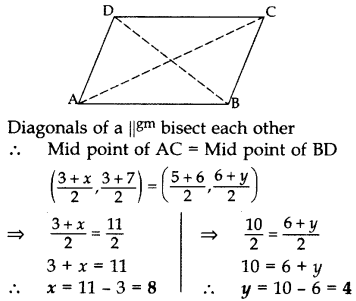
If (3, 3), (6, y), (x, 7) and (5, 6) are the vertices of a parallelogram taken in order, find the values of x and y.
Year of Question: (2011D)

Solution:
Let A (3, 3), B (6, y), C (x, 7) and D (5, 6).

Question 66.
Find the area of the quadrilateral ABCD whose vertices are A(-3, -1), B(-2, -4), C(4, -1) and D(3, 4).
Year of Question: (2011D, 2012OD)

Solution:

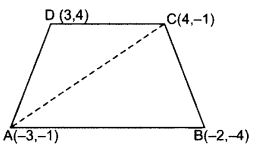
Area of ∆ = 1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
∴ Area of ∆ABC
= 1/2[(-3)(4 + 1) + (-2){-1 - (-1)} +4{-1 - (- 4}}]
= 1/2[9+ 0 + 12] = 21 sq. units .(i)
∴ Area of ∆ACD
= 1/2[-3(-1 - 4) + 4{(4 - (-1)} + 34{-1 - (-1)}]
= 1/2 [15 + 20 + 0]
= 1/2[15 + 20] = 35/2 sq. units
∴ar(quad. ABCD) = ar (∆ABC) + ar(∆ACD)
= 21/2+35/2 .[From (i) & (ii)
= 56/2 = 28 sq. units

Question 67.
The three vertices of a parallelogram ABCD are A(3, 4), B(-1, -3) and C(-6, 2). Find the coordinates of vertex D and find the area of ABCD.
Year of Question: (2013D)

Solution:

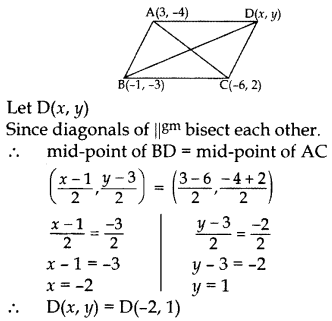
Area of ∆ = 1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
∴ Area of ∆ABC
= 1/2 [3(-3 - 2) + (-1)(2 + 4) + (-6)(+4+3)]
= 1/2 [-15 - 6 +6] = -15/2
= 15/2 sq. units .[∵ ar of A cannot be -ve.
Since diagram of a parallelogram divides it into 2 equal areas.
∴ ar( ‖gm ABCD) = 2(area of ∆ABC) = 2(15/2)
= 15 sq. units

Question 68.
If the points A(1, -2), B(2, 3), C(-3, 2) and D(-4, -3) are the vertices of parallelogram ABCD, then taking AB as the base, find the height of this parallelogram.
Year of Question:(2013OD)

Solution:

1st method. A(1, -2), B(2, 3), D(-4, -3)
.. Area of ∆ABD
= 1/2 [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
= 1/2 [1(3 + 3) + 2(-3 + 2) + (-4)(-2 - 3)]
= 1/2 [6 - 2 + 20) = 24/2 sq.units
ar(∆ABD) = 12 sq.units
= 1/2 × AB × DM = 12 sq.units .[Area of ∆ = 1/2 × Base × Altitude

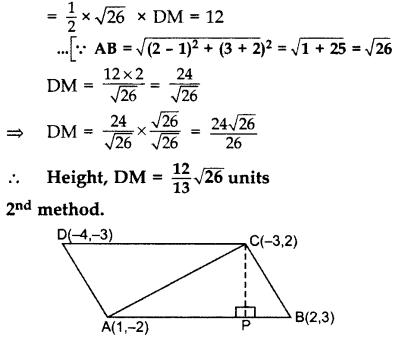
Area of ∆ABC = 1/2 [x2(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
= 1/2[1(3 - 2) + 2(2 + 2) + (-3)(-2 - 3)] = 1/2[1 + 8 + 15] = 12 sq. unit Area of ∆ABC = 12 ⇒ 1/2 × AB × CP = 12 .[Area of ∆ = 1/2 × Base × Height

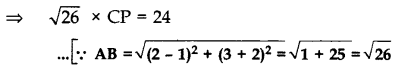
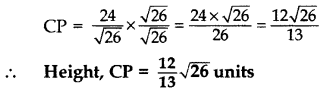
Question 69.
Find the value of k, if the points P(5, 4), Q(7, k) and R(9, - 2) are collinear.
Year of Question:(2011D)

Solution:
Given points are P(5, 4), Q(7, k) and R(9, -2).
x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2) = 0 .[∵ Points are collinear
∴ 5 (k + 2) + 7 (- 2 - 4) + 9 (4 - k) = 0
5k + 10 - 14 - 28 + 36 - 9k = 0
4 = 4k ∴ k=1

Question 70.
If P(2, 4) is equidistant from Q(7, 0) and R(x, 9), find the values of x. Also find the distance PQuestion
Year of Question:(2011D)

Solution:

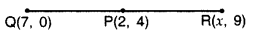
PQ = PR .[Given
PQ2 = PR2 . [Squaring both sides
∴ (7 - 2)2 + (0 - 4)2 = (x - 2)2 + (9 - 4)2
⇒ 25 + 16 = (x - 2)2 + 25
⇒ 16 = (x - 2)2
⇒ ±4 = x - 2 .[Taking sq. root of both sides
⇒ 2 ± 4 = x
⇒ x = 2 + 4 = 6 or x = 2 - 4 = -2

Question 71.
Find the point of y-axis which is equidistant from the points (-5, -2) and (3, 2).
Year of Question:(2011D)

Solution:
Similar to Question 26, Page 103.

Question 72.
Point M(11, y) lies on the line segment joining the points P(15, 5) and Q(9, 20). Find the ratio in which point M divides the line segment PQuestion Also find the value of y.
Year of Question:(2011OD)

Solution:
Similar to Question 62, Page 110.

Question 73.
Find the coordinates of a point P, which lies on the line segment joining the points A(-2, -2) and B(2, -4) such that AP = 3/7 AB.
Year of Question:(2012OD)

Solution:

AP = 3/7 AB .(Given)
AP/AB=3/7
Let AP = 3K, AB = 7K
BP = AB - AP = 7K - 3K = 4K
∴ AP/AB=3K/4K=3/4
Using Section formula, we have
P(6-8/3+4,-12-8/3+4)⇒(-2/7,-20/7)

Question 74.
Find the value of k, for which the points A(6,-1), B(k, -6) and C(0, -7) are collinear.
Year of Question:(2012OD)

Solution:
Similar to Question 69, Page 112.

Question 75.
Find the value of p, if the points A(1, 2), B(3, p) and C(5, -4) are collinear.
Year of Question:(2012OD)

Solution:
Similar to Question 69, Page 112.

Question 76.
Find the value of x for which the points (x, -1), (2, 1) and (4, 5) are collinear.
Year of Question:(2013D)

Solution:
Similar to Question 69, Page 112.

Question 77.
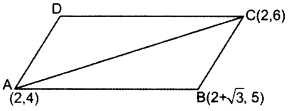
Find the area of a parallelogram ABCD if three of its vertices are A(2, 4), B(2 + √3, 5) and C(2,6).
Year of Question:(2013OD)

Solution:

Area of ∆ABD
= 1/2 [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
= 1/2 [2(5 - 6) + (2 + √3)(6 - 4) + 2(4 - 5))
= 1/2 (-2 + 4 + 2√3- 2)
= 1/2 (2√3) = √3
Since diagonal of a ‖gm divides it into two equal areas.
Area of ABCD (‖gm) = 2(Area of ∆ABC)
= 2√33 sq. units

Question 78.
If A(-3,5), B(-2, -7), C(1, -8) and D(6, 3) are the vertices of a quadrilateral ABCD, find its area.
Year of Question:(2014OD)

Solution:
Similar to Question 66, Page 111.

Question 79.
A(4, -6), B(3, -2) and C(5, 2) are the vertices of a ?ABC and AD is its median. Prove that the median AD divides AABC into two triangles of equal areas.
Year of Question:(2014OD)

Solution:
Similar to Question 56, Page 109.

Question 80.
If A(-, 8), B(-3,-4), C(0, -5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
Year of Question:(2015D)

Solution:
Similar to Question 66, Page 111.

Question 81.
If P(-5, -3), Q(-4, -6), R(2, -3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
Year of Question:(2015D)

Solution:
Similar to Question 66, Page 111.

Question 82.
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
Year of Question:(2015OD)

Solution:
Similar to Question 57, Page 109.

Question 83.
The x-coordinate of a point P is twice its y coordinate. If P is equidistant from Q (2, -5) and R(-3, 6), find the coordinates of P.
Year of Question:(2016D)

Solution:
Let the point P be (2k, k), Q(2,-5), R(-3, 6)

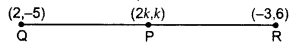
PQ = PR .Given
PQ2 = PR2 .[Squaring both sides
(2k - 2)2 + (k + 5)2 = (2k + 3)2 + (k - 6)2 .Given
4k2 + 4 - 8k + k2 + 10k + 25 = 4k2 + 9 + 12k + k2 - 12k + 36
⇒ 2k + 29 = 45
⇒ 2k = 45 - 29
⇒ 2k = 16
⇒ k = 8
Hence coordinates of point P are (16, 8).

Question Papers / Notes Download

Videos